티스토리 뷰

인공지능

[논문번역] Playing Atari with Deep Reinforcement Learning 논문 설명/요약

망나니개발자 2020. 2. 10. 14:54

0. Abstract

[ Abstract ]

High-Dimensional Sensory Input으로부터 Reinforcement Learning을 통해 Control Policy를 성공적으로 학습하는 Deep Learning Model을 선보입니다.
이 모델은 Atari는 CNN 모델을 사용하며, 변형된 Q-learning을 사용하여 학습되었습니다.
여기서 Q-learning이란 input이 raw pixels이고, output은 미래의 보상을 예측하는 value function입니다.
실제로 게임을 학습할 때, 스크린의 픽셀값들을 입력으로 받고, 각 행위에 대해 점수를 부여하고, 어떤 행동에 대한 결과값을 함수를 통해 받게 됩니다.
아타리는 2600개가 넘는 다양한 게임을 학습시키는데 동일한 모델과 학습 알고리즘을 사용하였고, 성공적인 결과를 보였습니다.

=> CNN에 대한 개념이 부족하신 분은 여기에서 참고하세요!

1. Introduction

Vision이나 speech와 같은 high-dimensional sensory inputs로부터 agent를 학습시키는 것은 RL의 오랜 과제였습니다. 이러한 데이터를 RL에 성공적으로 적용시킨 사례들은 Linear한 value function이나 policy representation에 결합된 hand-crafted features에 많이 영향을 받았습니다. 또한 이러한 Feature들의 quality에 성능 역시 많이 좌우되었습니다. 딥러닝이 발전함에 따라 Vision, Speech와 같은 고차원의 데이터들을 추출하는 것이 가능해졌습니다. 딥러닝에서는 이러한 고차원의 데이터들을 입력으로 사용하여 CNN, Multi-Layer Perceptrons, restricted Boltzmann machines, recurrent neural networks 등을 통해 지도 및 비지도학습에 사용하였습니다. 결과는 성공적이였고, 딥러닝을 강화학습에 도입하는 연구를 진행하게 되었습니다.

=> Deep Learning과 Reinforcement Learning에 대한 개념이 부족하신 분은 여기에서 참고하세요!

그러나 딥러닝을 강화학습에 적용하는 과정에서 몇가지 문제점을 발견하게 되었습니다.

대부분의 DL Application은 손으로 label된 많은 양의 traning데이터를 필요로 합니다. 반면에 RL은 sparse, noisy, delayed한 reward signal라는 scalar 값을 통해 학습을 해야 합니다. => 딥러닝은 input에 대한 결과가 직접 작성되어 계산의 시간이 적지만, RL에서는 어떠한 행위를 하면 Trial and Error를 통해 그 행위에 대한 결과를 알기까지 시간이 필요한데, 이러한 Delay는 어려움을 자아낸다.
딥러닝 알고리즘에서 각 데이터들은 독립적인 반면, 강화학습에서는 하나의 행위가 다른 것들과 연관성이 높다는 것이다. => 현재 상태의 행동이 다음 상태의 보상에 영향을 주는 등 상호연관성이 매우 높다.
RL에서는 알고리즘이 새로운 behavior를 배울때마다 data의 distribution이 변하게 되는데, 이것은 데이터의 분포가 고정되어 있다고 가정하는 딥러닝의 Assumption과 충돌하여 문제가 될 수 있습니다.

이 논문에서는 CNN이 복잡한 RL환경에서 원시 비디오로부터 성공적인 Control Policy를 학습할 수 있음을 증명합니다. CNN은 변형된 Q-Learning을 통해 학습되며, weight를 update하기 위해 stochastic gradient descent를 사용합니다. 또한 correlated data와 non-stationary distributions의 문제를 약화시키기 위해 Experience Replay Memory을 사용하는데, 이것은 무작위로 이전의 transition을 추출하여 training distribution이 원활해지게 합니다.

=> Q-Learning에 대한 개념이 부족하면 여기를, SGD에 대한 개념이 부족하면 여기를, Replay Memory에 대한 개념이 부족하면 여기를 참고해주세요!

DeepMind는 하나의 Neural Network를 만들어 가능한 많은 게임을 학습시키는 것을 목표로 하였고, 게임에 대한 특정 정보나 게임의 우위를 위한 데이터 등을 제공하지 않았습니다. 오직 비디오의 시각 데이터와 Reward 그리고 터미널로부터 오는 신호 그리고 가능한 몇개의 행등으로만 학습을 진행하였습니다. 또한 다양한 게임들에 대해 동일한 Network Architecture와 Hyperparameter를 사용하였다.

2. Background

Agent가 환경($E$, Atari Emultator) 와 상호작용하는 task를 생각해보겠습니다. 각 time-step마다 Agent는 할 수 있는 행동( $a_T$) 들 중에서 한가지를 선택하게 됩니다. Action이 전달되면 Emulator는 내부 상태를 변경하고 게임 점수를 수정하게 됩니다. 여기서 Agent는 게임의 내부 상태를 알 수 없고, 단지 현재 화면을 나타내는 raw pixel 의 vector로 이루어진 이미지와 game score의 변화를 나타내는 reward($r_t$) 만을 전달받습니다.
=> 즉, 매 time-step마다 Agent가 action($a_t$) 를 선택하면 Emulator를 통해 state를 수정하고 reward($r_t$)가 return 됩니다.

하지만 게임의 점수는 현재의 행동뿐만 아니라 이전에 거쳤던 일련의 행동에 의존하여 결정되고, 행동에 대한 피드백은 수천 회의 time-step이 진행된 후에 받게됩니다.

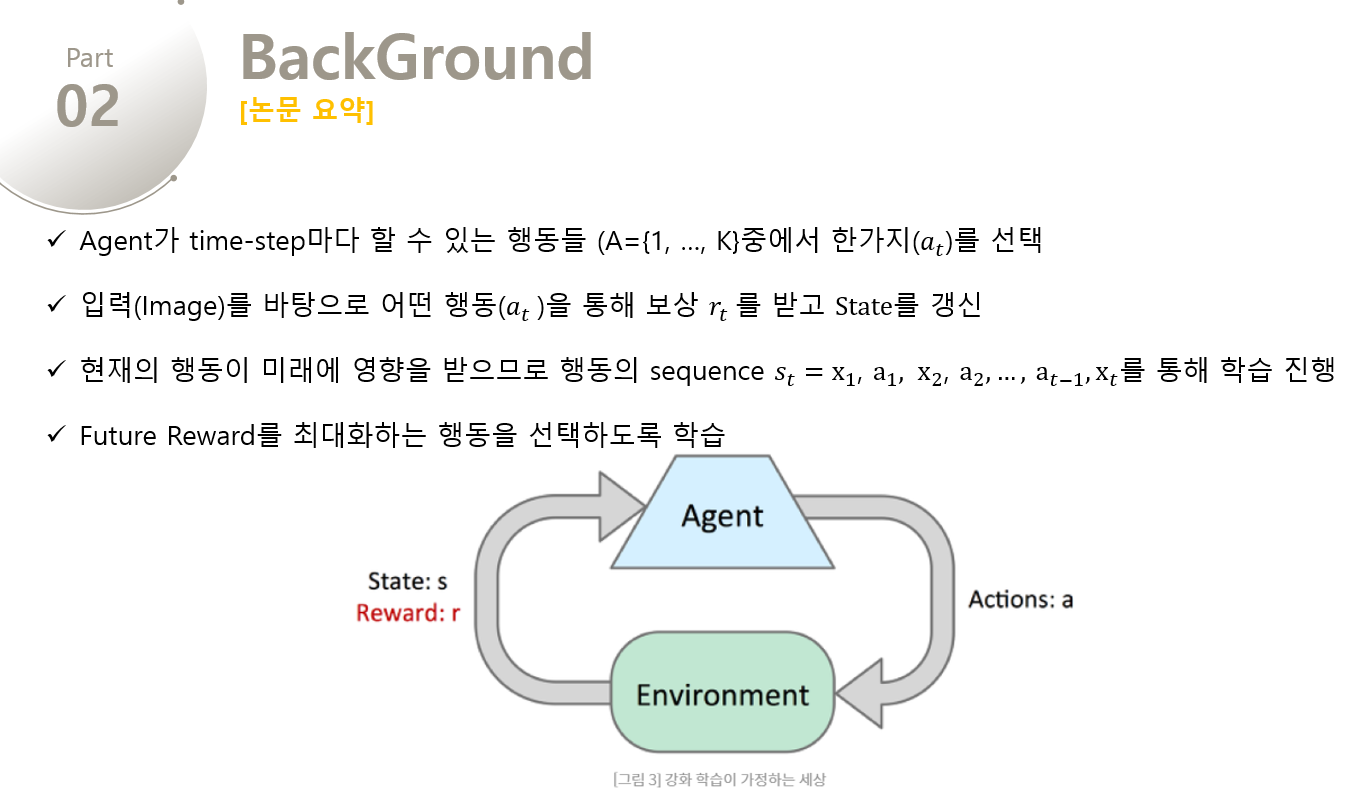
하지만 Agent는 오직 현재의 장면 만을 관찰하기 때문에, 전체적인 상황을 이해하기 힘듭니다. 그래서 이를 해결하기 위해 action의 sequence를 관찰하고 이를 통해 학습을 진행합니다. 이러한 Formalism은 크지만 유한한 Markov Decision Process(MDP)을 야기하는데, 여기서 각 시퀀스는 별개의 상태에 해당한다. 결과적으로 우리는 MDP에 standard한 reinforcement learning method를 적용할 수 있고, 이것은 시간 t에서의 상태를 표현하기 위해 전체 시퀀스를 사용함을 의미합니다. 그래서 Agent의 목표는 Future Reward을 극대화시키는 방식으로 action을 선택하고 이를 Emulator에 전달는 것입니다. 시간이 오래 지날수록 그 reward의 가치는 점점 내려가는데, 이를 적용시키기 위해 discount factor $r$이 정의된다.

=> Markov Decision Process과 Discounted Future Reward에 대한 개념이 부족하면 여기를 참고해주세요!

시간 t에서 discounted factor가 정의된 reward를 $R_t$라고 할 때, 해당 값은 아래와 같이 정의합니다.
$$R_t = \sum_{t`=t}^{T}r^{t`-t}{r_{t^{`}}}$$
이 식에서 T는 game이 종료되는 time이고, 현재의 시점에서 종료 시점까지 reward값에 reward factor의 t'-t 지수 값을 한게 됩니다. 그리고 어떤 일련의 행동(s)를 파악한 후에, 취한 행동(a)을 통해 얻을 수 있는 Expected 최대값을 반환하는 최적의 action-value function인 $Q^{*}(s, a)$를 정의하였는데 해당 함수는 아래와 같습니다. 여기서 $\pi$ 는 $s_t$ 에서 $a_t$ 를 Mapping하는 Policy Function이다.
$$Q^{*}(s, a) = max_{\pi} E[R_t | s_t = s, a_t = \alpha, \pi ]$$
최적의 Q-Function은 Bellman Equation이라는 중요한 특성을 따른다.

=> Bellman Equation에 대한 개념이 부족하면 여기를 참고해주세요!

이 방정식은 sequence $s'$의 다음 time-step에서 최적의 $Q^{*}(s, a)$ 값이 모든 모든 행동 $a'$ 에 알려져 있다면, 최적의 전략은 $r + \gamma Q^* (s^\prime, a^\prime)$ 의 Expected Value를 최대화하는 것이다. 이를 수식으로 표현하면 다음과 같다.

$$Q^*(s,a) = \mathbb E_{s^\prime \sim \mathcal E} \bigg[ r + \gamma max_{a'} Q^* (s^\prime, a^\prime) ~\big|~ s,a \bigg].$$

많은 강화학습 알고리즘에서는 Q-Function을 Estimate하기 위하여 Bellman Equation을 Iterative Update한다. Value Iteration 알고리즘은 매 i번째 Iteration마다 아래와 같은 Procedure를 수행하게 된다.
$$ Q_{i+1} (s,a) = \mathbb E \bigg[ r + \gamma Q_i (s^\prime, a^\prime) ~\big|~ s,a \bigg] $$
이런 Value Iteration Algorithm은 MDP에서 $Q_i \to Q^* \mbox{ as } i\to\infty$ 라는 것이 알려져있다.

그러나 action-value function은 각 sequence마다 독립적으로 측정되기 때문에, 이런 방식은 실제로 impractical(비현실적)하다. 대신 function approximator를 사용하여 action-value function을 적절히 approximate 시킨다.
$$ Q(s,a;\theta) \simeq Q^* (s,a). $$
일반적으로는 Linear Function으로 Approximate 하지만, 간혹 Non-Linaer Function으로 Approximate하는 경우도 있다. neural network function approximator로 weight $\theta$ 를 사용하는 것을 Q-network라고 한다. Q-Network는 each iteration마다 바뀌는 Loss function $L_i(\theta_i) $를 최소화시킴으로써 학습을 한다.
$$ L_i (\theta_i) = \mathbb E_{s,a\sim \rho(\cdot)} \bigg[ \big(y_i - Q(s,a;\theta_i) \big)^2 \bigg], \mbox{where, }y_i = \mathbb E_{s^\prime \sim \mathcal E} \bigg[r + \gamma \max_{a^\prime} Q(s^\prime, a^\prime;\theta_{i-1}) ~\big|~ s, a \bigg] $$

여기서 $y_i$ 는 iteration i의 target value이며 $\rho(s,a)$ 는 behaviour distribution으로 sequence s에 대해 action a의 probability distribution이다. $\theta_{i-1}$ 은 Loss function $L_i(\theta_i) $를 optimize할 때 fixed 되는데, 학습이 진행되기 전에 고정되었던 supervised learning과는 대조된다. 이러한 네트워크의 Gradient는 아래와 같다.
$$\nabla_{\theta_i} L_i (\theta_i) = \mathbb E_{s,a\sim \rho(\cdot); s^\prime \sim \mathcal E} \bigg[ \big( r + \gamma \max_{a^\prime} Q(s^\prime, a^\prime; \theta_{i-1}) - Q(s,a;\theta_i) \big) \nabla_{\theta_i} Q(s,a;\theta_i)\bigg]$$
Deep-Q Learning 알고리즘은 $\mathcal E$ 와 별도로 작동하는 model-free 알고리즘이며, Behavior Policy와 Learning Policy를 별도로 두는 Off-Policy를 사용한다.$\epsilon$의 확률로 random action을 선택하고, .$1 - \epsilon$의 확률로는 $a = max_aQ(s,a,;\theta)$ 인 greedy strategy를 따른다.
=> 일반적으로 RL의 데이터들은 correlation이 상당히 높다. 그러므로 이러한 data들간의 correlation을 깨기 위해 일정한 확률로 random action을 선택하고, 남은 확률로는 greedy strategy를 따라 행동을 선택한다.

=> E-greedy Algorithm에 대한 개념이 부족하면 여기를 참고해주세요!

Loss Function 이란?

$Loss = \sum{(Q_{target}-Q})^{2}$ 에서 $Q_{target}$ 은 다음 상태에 대한 Q의 예측값으로, s'과 s''을 고려한 것이며, Q는 현재의 예측값으로 상태나 행동들을 고려하여 최대의 결과를 추출한다. $Q=r+\gamma(max( Q(s', a')))$ 에 해당한다.

3. Related Work

이전에 Reinforcement가 적용되었던 가장 유명한 사례는 TD-gammon이다. 강화학습을 통해 스스로 플레이 방법을 터득하고, Q-learning과 유사하게 Model-Free한 구조로, Multi-Layer Perceptron with One Hidden Layer의 Network를 가졌다.

하지만 TD-gammon의 방식을 GO나 Chess에 적용을 할 때면 실패하였고, 이러한 접근법은 TD-Gammon에만 최적화되었으며 어쩌면 주사위의 확률이 우연하게 탐험을 돕고, value funtion을 smooth하게 만들어 주었다는 착각을 불러일으켰다.

또한 Q-Learning과 같은 Model-Free Reinforcement Learning 알고리즘을 Non-Linear Function Approximator나 Off-Policy Learning에 적용시키면 Q-network가 발산하며, 수렴을 위해 주로 Linear Function Approximators에 초점을 두고 RL이 진행되도록 초래하였다.

그리고 최근에야 DL과 RL을 융합시키는 분야가 부활하게 되었다. Deep Neural Network는 환경 $E$ 를 측정하기 위해 사용되게 되었고, restricted Boltzmann 기계들은 value function이나 policy를 측정하기 위해 사용되기 시작하였다. 게다가 발산문제는 gradient temporal-difference에 의해 다루어지게 되었고, 이것은 non-linear function approximator로 fixed policy를 사용할 때나 제한적인 Q-Learning의 변형을 활용하여 linear function approximation과 함께 control policy를 학습할 때 수렴함을 증명하였다. 그러나 이것은 nonlinear control 까지 확정되지는 않은 상태였다.

우리의 접근법과 가장 유사했던 이전의 작업으로는 Neural fitted Q-Learning(NFQ)가 있다. NFQ는 Q-Network의 Parameter들을 갱신시키기 위해 RPROP 알고리즘을 사용하여 2번 방정식에서의 Loss Function을 최적화시켰다. 그러나 이것은 Iteration을 돌기 위해 많은 계산 양을 필요로하는 Batch Gradient Descent를 사용하였지만, 이 논문에서는 Stochastic Gradient Descent를 사용하여 Iteration을 돌기 위해 필요한 계산 양을 줄였고, 큰 Data-Set까지 학습을 Scale-up 시켰다. NFQ는 또한 처음으로 deep autoencoder를 사용함으로써 task의 low dimensional representation을 학습하였고, 시각입력을 사용함으로써 real-world control task를 성공적으로 NFQ 알고리즘에 적용하였다. 그러나 이와 반대로 우리는 시각적 입력으로부터 직접적으로 철저한 강화학습을 적용시켰고, 결과적으로 Action-Value를 판별하는 것과 같은 특징들을 학습하였다.

RL 플랫폼으로 사용된 Atari 2600 에뮬레이터는 visual features와 linear function approximation을 standard RL에 적용시켰던 [3] 논문에서부터 사용되기 시작하였습니다. 결과적으로 많은 수의 특징들을 lower-dimensional space에 적용시킴으로 결과는 개선되었다. HyperNEAT evolutionary architecture는 Atari Platform에도 적용되었으며, 이 플랫폼은 각 게임마다 전략을 나타내는 Neural Network를 발전시키는데 사용되었습니다. Emulator의 리셋 기능을 사용하여 결정을 내리는 Sequence에 대해 반족적으로 교육을 받았을 때, 이러한 전략은 여러 아타리 게임에서의 디자인 결함을 악용할 수 있었습니다.

4. Deep Reinforcement Learning

Computer Vision과 Speech Recognition에서 이뤄낸 최근의 성과는 매우 큰 training sets를 활용하여 deep neural network를 효과적으로 훈련시킨 결과였다. 대부분의 성공적인 approaches는 Stochastic Gradient Descent를 기반으로 lightweight update함으로써, raw input들로부터 직접 학습된 것들이였다. Deep Neural Network에 충분한 양의 Data를 제공함으로써, handcrafted된 features보다 많은 representation들을 학습할 수 있었고, 이러한 성공들을 바탕으로 RL에 대한 우리의 접근법을 생각해냈다. 우리의 목표는 RL 알고리즘을 Deep Neural Network와 연결하여 RGB Image들에 직접적으로 작동하고, Stochastic Gradient Updates를 사용하여 Traning Data를 효율적으로 처리하는 것이다.

TD-Gammon과 달리 우리는 experience replay라는 기술을 활용하였는데, Agent가 매 Time-Step마다 했던 Experience(Episode)들을 Dataset에 저장을 시키고, 수많은 Episode들이 replay memory에 쌓이게 된다. 그리고 알고리즘 내부에서 샘플들이 저장된 풀로부터 임의로 하나를 샘플링하여 학습(Q-Learning, Mini-Batch)에 적용시켰다. 이후에(experience replay 후) Agent는 e-greedy policy에 따라 행동을 선택하고 수행한다. Neural Network의 입력으로써 가변적인 history를 사용하는 것은 어렵지만, Deep-Q Algorithm에서는 $\phi$ 함수를 사용하여 고정 길이의 history를 입력으로 사용한다.

이러한 DQN은 기존의 Q-Learning보다 아래와 같은 장점을 지닌다.

each step의 Experience가 잠재적으로 많은 weight update에 재사용되므로, Experience를 weight update 한번만 사용하는 기존의 방법보다 훨씬 data efficiency 하다.
연속적인 sample들로부터 학습을 진행하는 것은 데이터들간의 high correlations때문에 비효율적이다. 하여 sample들을 e-greedy 알고리즘을 통해 randomize하여 sample들의 high correlations를 break하여 update의 효율성을 높인다.
기존의 on-policy를 통해 학습을 하면, 매개변수가 학습된 다음 데이터 샘플을 결정한다. 예를 들어, 만약 보상을 극대화하는 행동이 왼쪽으로 움직이는 것이라면 training sample들은 왼쪽의 샘플들로 dominate 될 것이다. 만약 극대화하는 행동이 오른쪽으로 바뀌면 traning distribution 역시 오른쪽으로 바뀔 것이다. 이런 것들을 통해 원하지않는 feedback loops가 발생하고, parameter들이 local minumum으로 수렴하거나 발산함을 파악할 수 있다. experience replay를 사용함으로써, behavior distribution이 균형을 이루게 되고 parameter의 발산이나 진동을 피하고 학습을 매끄럽게 진행한다. 또한 experience replay를 통해 학습하기 위해서는 Q-Learning의 choice를 원활히하는 off-policy를 사용해야 한다. 왜냐하면 Behavior Policy의 Parameter $\epsilon$ 과 Learning Policy의 Parameter $\theta$ 가 다르기 때문이다.

DQN에서는 replay memory 안에 마지막 N개의 exprience만을 저장하고, update를 하기위해 무작위로 Data Set으로부터 추출한다. 이러한 접근법은 Memory Buffer가 중요한 Transition에 차별점을 두지 않고 항상 제한된 크기 N의 버퍼에 최근의 Transition을 덮어 씌운다는 접에서 한계가 있다. 마찬가지로, uniform sampling은 replay memory안의 모든 transition에 동일한 중요성을 부여한다. 더욱 정교한 Sophisticated Sampling 전략은 우선순위를 매기는 것과 유사하게 우리에게 가장 중요한 Transition을 중요시 할 것이다.

1) replay memory D와 이것의 capacity를 N으로 초기화한다.
2) action-value function Q를 random weight로 초기화한다.
3) episode를 1~M까지 반복한다.
4) sequence s1을 t=1일때의 이미지 $x_1$으로 초기화하고, 전처리과정을 통해 $\phi_1$ 을 구한다.
5) t를 1~T까지 반복한다.
6) e-greedy 알고리즘을 따라 무작위 action 또는 이전에 최선의 결과를 냈던 action 중 하나를 $a_t$ 선택한다.
7) emulator에서 action $a_t$ 를 수행하고, reward $r_t$와 다음 image $x_{t+1}$ 를 observe한다.
8) 그리고 현재의 State $s_t$, 현재의 Action $a_t$, 새로운 image인 $x_{t + 1}$ 을 $s_{t + 1}$ 로 저장하고, $s_{t + 1}$ 에 대해 pre-processing을 한다.
9) 그리고 replay memory D에 현재의 상태를 전처리한 값 $\phi_t$, $a_t$, $r_t$, $\phi_{t + 1}$ 을 저장한다.
10) D에 저장된 Sample들 중에서 minibatch의 개수만큼 random하게 뽑는다.
11) 여기서 $y_j$를 정의하는데, 전처리한 결과인 $\phi_{j+1}$ 이 목표 지점에 도달하면 $r_j$ 로, 목표지점이 아니라면 $r_j + \gamma max_{a'} Q(\phi_{j+1}, a';\theta)$ 로 설정한다.
12) 그리고 방정식 3을 따라 Loss Function을 정의하고 gradient desenct를 수행한다.

4.1 Preprocessing and Model Architecture

[ Preprocessing ]

128 color palette를 가진 210 * 160 pixel images인 raw Atari frames로 직접 작업하는 것은 정말 많은 계산양을 필요로 한다. 그래서 먼저 input의 dimensionality를 줄이는 basic preprocessing step을 적용한다. 이러한 과정은 먼저 RGB로 표현된 이미지를 Gray-Scale로 변환하고, 110 * 84의 이미지로 down-sampling 시킨다. 이후에 게임의 진행 부분만 보이도록 84 * 84로 잘라내서 Final Input값을 추출한다. 이 알고리즘을 적용하기 위해서는 마지막 84 * 84로 잘라내는 기술이 반드시 필요한데, 사용하는 GPU에서 정사각형 사진만 GPU 연산이 가능하기 때문이다. 위의 알고리즘의 전처리 함수인 $\phi()$ 에서 마지막 4개의 frames만 전처리를 하여 Stack에 넣어두고, 이를 입력에 대한 Q-function의 값을 구하기 위해 사용한다.

=> 4개의 프레임이 1개의 화면을 구성하기에 4개의 프레임을 기준으로 처리한 것

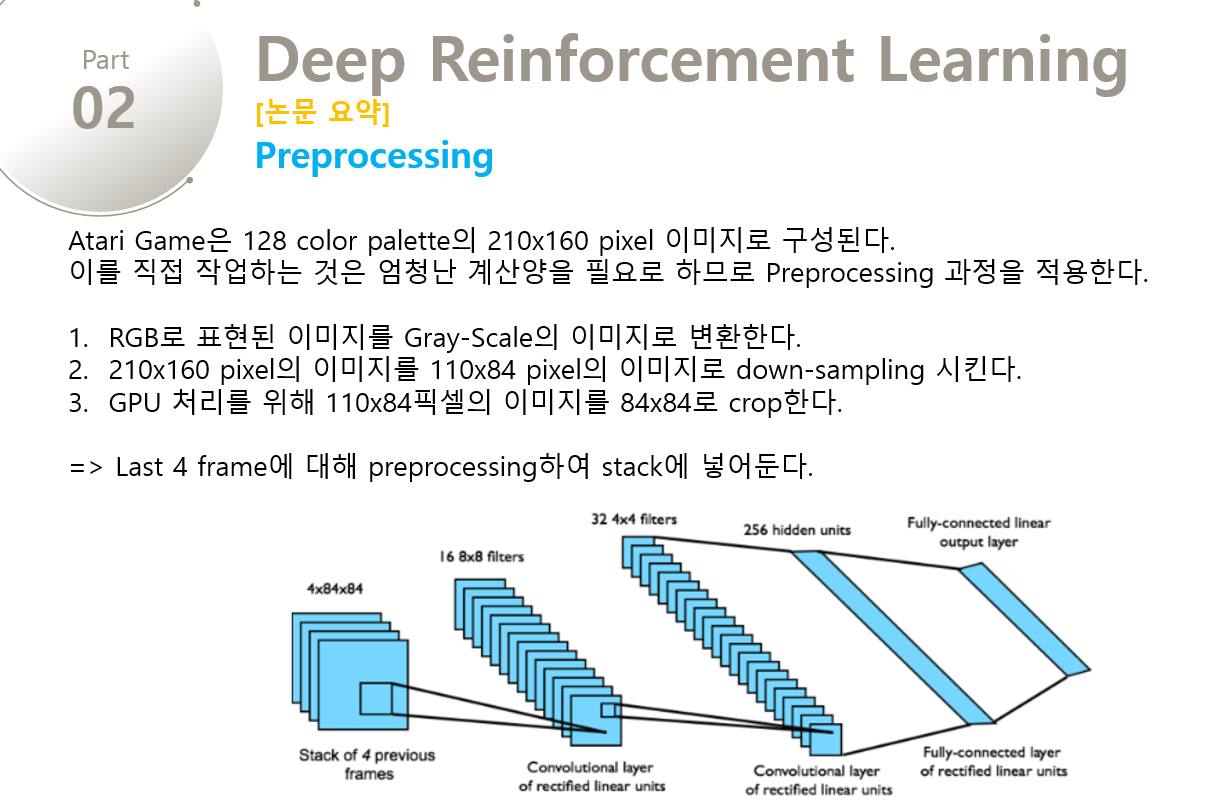
[ Model Architecture ]

Q-Value를 구하는 방법으로는 2가지가 있다.

istory와 action을 input으로 하고, output으로 history와 그 action에 대해 예측된 Q-value를 구하는 것
history만을 input으로 하여 output으로 각 행동에 대해 예측된 Q-Value를 구하는 것

1번을 사용하면 입력으로 들어온 action에 대해 seperate forward pass연산을 진행해야 하고, action의수가 증가함에 따라 linear하게 연산의 양도 증가하는 단점이 있다. 그래서 2번의 방법을 사용하는데, Neural Network의 입력으로 state를 사용하여 각 state에서 수행가능한 모든 Action에 대한 Q-value를 계산하기 때문에 좀 더 효율적이다. 우리는 어떤 상태를 입력으로 주고 원하는 행동에 대한 Q-value를 사용하면 된다. 즉, 주어진 상태에서 가능한 모든 Action에 대한 Q-value값을 한번의 single forward pass로 처리하는 이점을 얻을 수 있다.

[ DNN Architecture ]

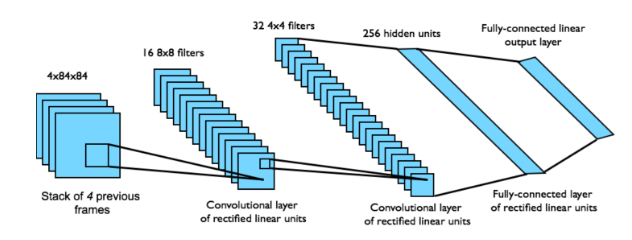
Neural Network의 Input은 $\phi$ 를 통해 전처리된 84 x 84 x 4 이미지(4 frames)이다.
첫 번째 Hidden Layer는 input image에 stride 4를 토함한 16 8x8(16 channels with 8x8 filters)로 합성곱 연산을 한 후에, rectifier non-linearity(ex. relu)를 적용한 것이다.
두번째 Hidden Layer는 stride 2를 포함한 32 4x4(32 channels with 4x4 filters)로 합성곱 연산을 하고 rectifier non-linearity(ex. relu)를 적용한 것이다.
마지막 Hidden Layer는 funnly-connected되고, 256개의 rectifier 유닛으로 구성된다.
최종적으로 Output layer는 각 수행가능한 행동에 대해 single output을 갖는 fully-connected linear layer이다.

5. Experiments

Experiment를 진행하면서 algorithm 및 hyper-parameter에 대한 3가지 setting이 나온다.

Reward Structure: Training을 하면서 Reward Structure에 한가지 변화를 주었다. 양의 보상은 1, 음의 보상은 -1, 변화 없음은 0으로 수정하였는데, 이를 통해 error derivatives(오류 도함수)의 스케일을 제한하고, 모든 게임에 동일한 learning rate를 적용할 수 있었다. 그러나 보상의 강도 역시 제한함으로써 에이전트의 성능의 제약을 가져올 수 있다.
RMSProp Algorithm & $\epsilon$ - greedy Algorithm: 최적화 알고리즘으로는 크기 32의 Minibatch을 RMSProp 알고리즘에 적용하였고, Behavior Policy로는 처음부터 100만번째 프레임까지는 1에서 0.1까지 동일한 비율로 감소하는 epsilone 값을 통해 e-greedy 알고리즘을 사용하였고, 이후에는 0.1로 고정하였다.
Frame Skipping Technique: Agent가 모든 Frame을 보고 Action을 취하는 것이 아니라 K번째 프레임을 보고 액션을 고르게 하였고, 마지막 행동은 skipped된 frames에 반복 적용시켰다. 액션을 선택하기 위해서는 많은 양의 계산을 필요로 하지만, 한 스텝을 forward하는 것은 훨씬 적은 연산을 필요로 한다. 그러므로 이러한 기술을 적용함으로써 실행시간은 같지만 약 k배 많이 게임을 진행시킬 수 있었다. Space Invaders를 제외한 모든 게임에서 k=4 로 정해주었는데, 이 게임에서는 게임 내부의 laser blinking과 문제가 생겨 특별히 k=3으로 처리를 하였다.

5.1 Training and Stability

Supervised Learning에서는 training sets와 validation sets를 통해 학습 중에 model의 성능을 쉽게 확인할 수 있었다. 그러나 Reinforcement Learning에서는 학습 중에 agent의 progress를 정확히 측정하는 것이 매우 어렵다. 이 논문에서 Evaluation Metric(평가의 척도)은 수많은 Games를 통해 평균화된 Reward를 토대로, Game 또는 Episode에서 평균적으로 얻은 보상이기 때문에 training동안에 모은 total reward를 주기적으로 계산해야 한다. 하지만 학습을 진행하면서 Policy의 Weights를 아주 조금 변화시키는 것이 state의 distribution에 큰 변화를 줄 수 있어서, 여기서 사용하는 average total reward metric은 때때로 noisy하다.

Figure2에서 왼쪽의 두 그래프는 Sequest, Breakout이라는 게임에서 학습을 하는동안 totalreward가 어떻게 변화하는지 보여준다. 두 그래프는 steady한 progress를 만들어내지 못했으며, 상당히 noisy하다. 하지만 Policy에 대한 Action-Value를 예측하는 Q-function은 상당히 stable한데, 이 함수는 Agent가 어떤 state에서 Policy를 따랐을 때, 얼마의 discounted reward를 얻을 수 있는지를 제공한다. 우리는 traning이 시작하기 전에 random policy를 적용하고 게임을 실행하여 몇개의 fixed state를 수집하였고 이런 state들에 대해 maximum predicted Q의 값을 도출하였다. 오른쪽의 두 그래프는 Average Predicted Q가 Agent를 통해 얻은 average total reward보다 훨씬 smooth하게 증가함을 보여주고, 다른 게임에서도 그래프를 그려보았을때 유사하게 smooth하게 증가하였다. 또한 실험에서 Q 값이 발산하는 경우는 없었다. 비록 반드시 수렴한다는 이론적인 검증은 없지만, 우리의 방식이 RL과 SGD를 사용하여 Neural Network를 stable하게 학습시킴을 알 수 있다.

5.2 Visualizing the Value Function

Figure3는 Seaquest 게임에서 학습된 value function을 시각화한 것이다. 해당 그림은 screen의 왼쪽에 enemy가 등장하였을 때, predicted value가 jump함을 보여준다(Point A). 적을 발견한 Agent는 Enemy를 향해 미사일을 발사하고, 발사된 미사일이 적을 맞추려고 할 때, predicted value가 오름을 보여준다(Point B). 그리고 적이 사라졌을 때 predicted value는 원래의 값으로 떨어지게 된다(Point C). Figure 3는 우리의 value function이 꽤나 복잡한 일련의 이벤트들에 대해 어떻게 진화해 나가야 할지 학습할 수 있음을 보인다.

5.3 Main Evaluation

Table1은 일정한 step까지 0.05의 e값을 갖는 e-greedy 알고리즘을 적용하여 다양한 학습 알고리즘을 적용한 결과이다. 아래의 표는 HNeat와 DQN에 대해 Episode의 실행 결과가 가장 좋았던 경우이다.

=> Sarsa: Sarsa알고리즘은 Atari task를 처리하기 위해 수작업으로 설계된 여러 가지 특징들을 위해 Linear Policy를 학습하였고, 가장 성능이 좋은 Feature Set의 점수를 report 하였다.

6. Conclusion

이 논문은 RL을 위한 새로운 Deep Learning Model을 소개하였고, 이 모델을 바탕으로 raw pixel들만을 입력으로 사용하여 2600가지가 넘는 아타리 게임을 위한 어려운 Control Policy를 학습하는 것이 가능함을 증명하였다. 또한 deep network의 학습을 쉽게하기 위해 Stochastic Minibatch Gradient Descent에 Experience Replay Memory를 적용한 Q-Learning의 변형을 소개하였다. 이러한 접근법은 Architecture나 Hyperparameter의 변화없이, 7개의 게임 중 6개의 게임에서 경이적인 결과를 도출하였다.

논문의 전체 PPT를 받기 원하시면 첨부파일을 참고해주세요!

Atari-발표자료.pdf

0.82MB

참고 자료

저작자표시 비영리 변경금지

'인공지능' 카테고리의 다른 글

[논문번역] Deep Reinforcement Learning with Double Q-learning 논문 설명/요약 (4)	2020.02.12
E-Greedy Algorithm(입실론 그리디 알고리즘)이란? (4)	2020.02.10
마르코프 의사결정 모델(MDP)이란? (0)	2020.02.09
Experience Replay Memory란? (0)	2020.02.09
Stochastic Gradient Descent(SGD)란? (0)	2020.02.09

공유하기 링크

페이스북
카카오스토리
트위터

공지사항

최근에 올라온 글

최근에 달린 댓글

Total

Today

Yesterday

링크

TAG more

« 2024/11 »
일	월	화	수	목	금	토
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

글 보관함

MangKyu's Diary