티스토리 뷰
오늘 읽고 설명할할 논문은 Deep Reinforcement Learning with Double Q-learning입니다. 이 논문의 선행 논문은 Playing Atari with Deep Reinforcement Learning 입니다. 이 논문을 읽지 않았다면 여기에서 참고하세요!
0. Abstract
[ Abstract ]
기존의 Q-Learning Algorithm은 특정 조건에서 action-value를 Overestimate(과평가)한다.
=> 보상받을 값에 따라서 다음 행동이 결정되는데, 잘못된 행동에 대한 action-value값이 과평가되면 잘못된 방향으로 학습이 진행될 수 있다.
기존의 Q-Learning은 이러한 overestimation때문에 몇몇 게임에서 좋은 성능을 보이지를 못했다. 우리가 제안하는 Double Q-Learning은 large-scale function estimation에 적용시킬 수 있는 학습법을 보여준다. 이를 DQN에 적용하여 overestimation을 줄일 수 있을 뿐 아니라, 여러 게임에서 좋은 성능을 낼 수 있다.
RL의 목표는 누적되는 미래의 Reward Signal을 최적화함으로써 sequential한 의사 결정 문제에 대해 올바른 policy를 학습하는 것이다. Q-Learning은 RL의 가장 유명한 알고리즘 중 하나이지만, estimated된 action-value에 대한 maximization step이 존재하여 비현실적인 action-value를 통해 학습하게 된다.
=> 기존의 Q-Learning은 어떤 상태(s')에서 취할 수 있는 행동들 중에서 maximum action value를 구하는 것을 목표로 학습을 진행한다.
물론 학습을 하다보면 부정확한 value로 estimate되는 것은 당연하다. 만약 모든 값들이 균등하게 over-estimate된다면 이것은 문제가 되지 않으며, 심지어 원하는 값에 대해 overestimate되는 것은 때로 좋은 결과를 불러일으킨다. 그러나 overestimate가 일정하게 되지 않고, 우리가 학습하기를 원하는 값에서 발생되지 않는다면 Policy에 안좋은 영향을 미치게 된다.
이 논문에서는 DQN의 Over Estimation이 Policy에 좋지 않은 영향을 미치며, 그것을 줄여야 함을 증명한다. 또한 Double DQN 알고리즘을 통해 Atari 게임에서 성능을 향상시킬 수 있음을 보여준다.

[ Overestimation 부가 설명 ]
어떤 대상을 근사(approximate)한다는 것은 어느 정도의 오차를 감안하고 대략적으로 측정한다는 것을 의미한다. optimal policy $\pi$ 를 따르는 action-value function $q_{\pi} (s', a')$ 에 Noise(Y)를 더한 값은 근사값$\hat{q}(s^\prime, a^\prime, W)$와 같고, 이를 정리하면 $\hat{q}(s^\prime, a^\prime, W) = q_{\pi}(s^\prime, a^\prime) + Y_{s^\prime}^{a^\prime}$ 와 같다. 이를 아래에서 좀 더 자세히 설명하도록 하겠다.
Q-Learing에서 현재 시점의 state s와 action a에 대응되는 value는 바로 다음 시점의 immediate reward$R_{t+1}$ 과 다음 state $s'$ 이 가질 수 있는 value의 최대값 discount($\gamma$)한 후에 더해서 구한다. 우리는 근사 함수와 근사 대상을 아래와 같이 표현할 수 있다.
$Q^{approx}(s, a) = R_{t+1} + \gamma max_a Q^{approx}(s^\prime, a)$
$Q^{target}(s, a) = R_{t+1} + \gamma max_a Q^{target}(s^\prime, a)$
근사값과 실제값의 차이(Z)는 평균이 0인 정규 분포를 따랐던 Noise와 달리 평균이 0이라는 속성을 갖지 않게되는데, 이러한 이유는 $Q^{approx}$ 가 max값만을 선택하기 때문입니다.
$Z_s = \gamma(max_a Q^{approx}(s^\prime, a) - max_a Q^{target}(s^\prime, a))$

1. Background
sequential decision problem을 해결하기 위해, 각각의 행동에 대한 optimal value(Expected sum of future rewards)의 추측값을 학습한다. 즉, 어떤 policy $\pi$ 를 따라 어떤 상태 $s$ 에서 행동 $a$ 를 했을 때의 값은 아래와 같다.
$$ Q_{\pi} = E[R_1 + \gamma R_2 + ... | S_0 = s, A_0 = a, \pi ]$$
그리고 이러한 행동들에 대해 optimal한 값은 여러 action-value 값 중에서 max값을 선택하는 것이다.
[ Double Q-learning ]
Q-Learning과 Deep Q Networks에서 사용되는 max 연산자는 action을 select하고 evaluate 하는데 같은 값을 사용한다. 그리고 이것은 overestimated된 값을 더욱 선택하게 하며, overoptimistic한 결과를 불러 일으킨다. 이러한 문제를 해결하기 위해 selection과 evaluation을 분리시키는 Double Q-Learning을 사용할 수 있다. 초기의 Double Q-Learning 알고리즘은 각 experience에 대해 $\theta$ 또는 $\theta'$ 중 하나의 weight만을 randomly update시키는 방식을 사용하였다. update를 할 때 마다 하나의 변수는 greedy-algorithm에서 행동을 선택하기 위해 update되고, 또 다른 변수는 action에 대한 Q-Value를 구하기 위해 update 된다.
기존의 Q 함수는 아래와 같다.
$Y_t^Q = R_{t+1} + \gamma max_{a} Q (s_{t+1}, a; \theta_{t}) $
위의 식을 select와 evaluation을 명확히 하기 위해 아래와 같이 변형할 수 있다.
$Y_t^Q = R_{t+1} + \gamma Q(S_{t+1}, argmax_{a} Q (s_{t+1}, a; \theta_{t}); \theta_t) $
그리고 Double Q-Learning에서는 아래와 같이 selection과 evaluation을 분리하여 표현한다.
$Y_t^Q = R_{t+1} + \gamma Q(S_{t+1}, argmax_{a} Q (s_{t+1}, a; \theta_{t}); \theta'_t) $
위의 그림상으로 $\theta_t$ 는 argmax에서 action을 선택하고, $\theta'_t $ 는 policy를 evaluate하는데 2개의 weights는 서로 switching하며 update된다.

2. Overoptimism due to estimation errors
우리는 overestimaion의 lower bound와 upper bound를 구할 수 있다.
=> 논문에 관련 식이 적혀있음
우리는 서로 다른 action에 의한 Estimation Error가 독립적이라고 생각해선 안된다. 이 논문에서는 value에 대한 estimate가 평균적으로 맞다고 하더라도, 어떠한 근원으로부터 온 estimation error가 true optimal values로 부터 멀어질 수 있음을 보여주기 때문이다.
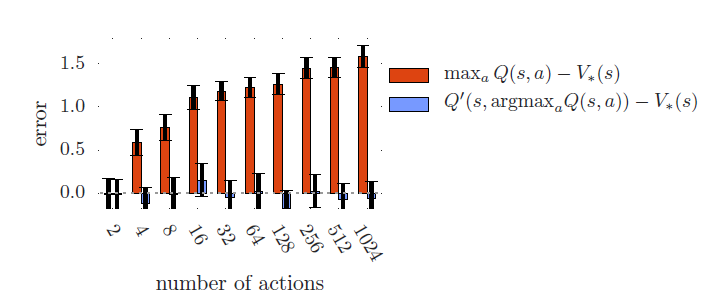
위의 그래프에서 보이듯이 Single Q-Learning에 해당하는 빨간 그래프는 number of actions가 증가함에 따라 overestimation이 증가하지만, Double Q-Learning에 해당하는 파란 그래프는 그렇지 않음을 보여준다.

이제 다시 function approximation으로 돌아와서, 각 state에서 10개의 action을 갖는 real-valued continous state space를 생각해보자. 간단히 말해, 우리가 고려하는 상황의 true optimal action values는 state에만 의존하여 각 state에서 모든 action은 같은 true value를 갖는다. 위와 같은 그래프에서 왼쪽 그래프들 중 보라색 선이 true value에 대한 그래프인데, 첫번째 True Value는 sin(s) 함수, 두번째, 세번째는 $$ 에 해당한다. 또한 왼쪽 그래프의 초록색 그래프는 single action에 대한 approximation에 해당하는데, 첫번째와 두번째 Estimation Function은 6차 방정식이고, 세번쨰 그래프는 9차 방정식이다. 각각의 Estimation Function들은 sampled states(초록 점들)에서의 True Value를 알고 있는 상태에서 구현되었다. 그럼에도 불구하고 첫번째와 두번째 그래프에서는 sampled states에서조차 부정확한 것을 확인할 수 있는데, 이것은 해당 Estimation Function의 차수가 낮아 충분히 Flexible하지 않기 때문이다. 세번째 그래프는 sampled states에서 True Value에 맞추기에 충분히 Flexible하지만 unsampled states에서의 정확성은 감소됨을 확인할 수 있다. 또한 sampled states의 왼쪽을 보면 다른 state들보다 거리를 두고 있는 것을 알 수 있는데, 이것은 더 큰 estimation error를 만들었다. 이렇게 특정 순간에 우리가 제한적인 데이터만을 지니는 것이 실제 학습할 때의 환경과 같고 Estimation Error는 실제 학습을 진행할 때 자주 발생하게 된다.
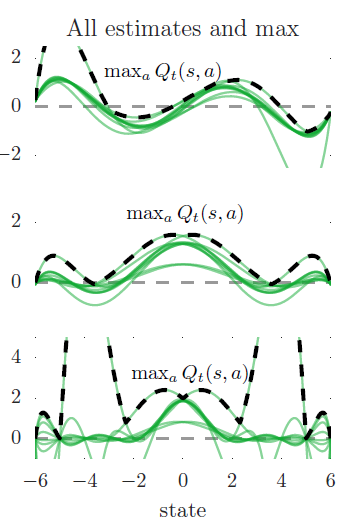
estimate에 대한 함수는 d-degree 방정식으로 앞에서 sample한 state에서 true value와 같은 값을 갖는다. 위의 첫 번째, 두 번째 그래프는 d=6이며, 세 번쨰 그래프는 d=9에 해당한다. sample들에서는 estimate와 true value가 정확히 일치하는데, 해당 state에서는 어떠한 noise도 존재하지 않으며 어떤 ground truth가 존재한다. 위의 그래프는 10개의 모든 행동에 대해 estimated action-value를 초록색으로 그렸고, 그 중에서 maximum값만 취한 것이 검은 색이 포함된 그래프이다. 아래 그림의 첫 번째, 두 번째 그래프에서 approximation은 flexible하지 않기 때문에 sampled states에서조차 부정확하다. 세 번째 그래프에는 충분히 flexible하여 sampled states에서 일치하지만 정확도가 줄어들게 된다. 당연히 true value function은 모든 action에 대해 같은 값을 같지만, 10개의 action에 대한 Estimation value의 값은 각각 다르다. 또한 maximum값은 true value보다 높게 나타나곤 한다.
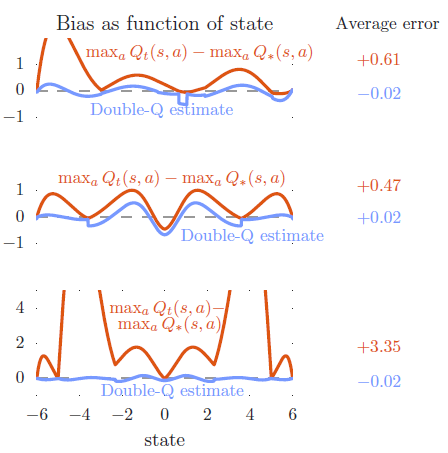
위의 주황색 그래프는 Maximum Estimation과 True Value의 차이를 보여주는 그래프로 upward bias를 지니기에 항상 positive한 값을 지닌다. 파란색 그래프는 Double Q-Learning을 활용한 Estimate인데, 평균적으로 거의 0에 근접하다. 그리고 이것은 Double Q-learning이 성공적으로 Q-Learning의 Overestimation을 줄였음을 보여준다.
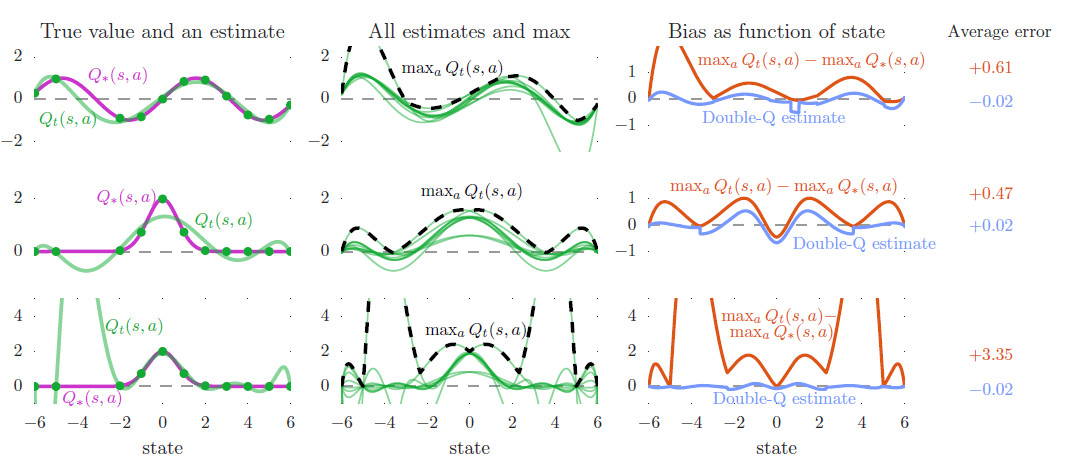
위의 각 row는 같은 실험에 대해 변형을 한 것이다. 첫 번째, 두 번째 그래프는 overestimation이 특정한 true-value function의 구조에 종속된 것 이 아니라는 것을 증명하기 위해 true-value function을 다르게 해 준 것이다. 두 번째, 세 번째 그래프는 function approximation의 flexibility를 다르게 해준 것이다. 왼쪽의 중간 그래프에서는 sampled states에서 조차 estimate가 부정확한데, 이것은 해당 function이 충분히 flexible하지 않기 때문이다. 왼쪽의 아래 그래프는 훨씬 flexible 하지만 sampled states가 아닌 곳에서는 더 높은 estimation error를 야기하고, 결과적으로 더 높은 overestimation을 초래한다. 실제 RL에서는 flexible parametric function approximator를 사용하는 경우가 많기에 이는 중요한 문제이다.
이 논문에서는 overestimation을 찾기 위해 statistical argument를 사용하지 않았다. 또한 우리는 inflexible function approximation에 의존하지 않았고, 가장 아래의 그래프는 flexible한 function approximation을 적용하여 모든 sample states에 대해 커버하였지만, 이것은 overestimation을 유발했다. 그리고 이를 통해 overestimation은 어느 상황에서나 발생할 수 있음을 알 수 있다.
위의 예시에서 보면, OverEstimation은 정확한 action-value 값을 갖는 상태에서도 발생한다. 이미 overoptimistic된 action-value값을 계속해서 내보내게 되면 overestimation을 propagate하게 되고, value estimates를 더욱 악화될 수 있다. 그러나 uniformly overestimating된 값들은 문제가 되지 않는다. 왜냐하면 다른 상태와 다른 행동에 대해 estimation error가 다르기 때문이다. overestimation을 bootstrap off 하게되면 다른 것보다 가치있는 state에 대한 잘못된 정보를 propagate하게 되고, directly 학습 policy의 quality에 영향을 미치게 된다.
overestimation: uncertainty
optimism: certainty
overestimation은 exploration bonus가 특정 state나 action에 대해 uncertain한 값으로 주어지는 optimism과 혼동되면 안된다. 여기서 overestimation은 update를 한 후에 발생하는 것으로, certainty하게 overoptimism을 유발한다. Optimism과 달리 uncertainty에도 불구하고, 이러한 overestimation은 최적의 policy를 학습하는데 방해가 될 수 있다. 그리고 우리는 policy quality가 받는 negative effect를 실험에서 확인할 수 있다.
3. Double DQN
Double Q-Learning의 기반이 되는 idea는 action selection과 action evaluation으로 max operation을 decomposing함으로써 overestimation을 줄이는 것이다. 비록 완전히 분리되지는 않지만, Network를 추가하지 않고 DQN 구조의 target network는 후보군의 value function을 제안한다.
Double Q-Learning과 DQN을 조합한 알고리즘을 Double DQN이라고 한다. Double Q-Learing과 달리 second network $\theta_{t}^{'}$ 현재 greedy policy의 evaluation을 위해 target network $\theta_{t}^{-}$ 로 replaced 되었다.
4. Empirical Results
이 섹션에서는 DQN의 overestimations에 대해서 분석하고, Double DQN이 value accuracy와 policy quality의 관점에서 성능이 좋아짐을 증명한다. 또한 이러한 접근법의 견고함을 테스트하기 위해, random start로 알고리즘을 평가한다. 그리고 목표는 screen의 pixel값만을 입력으로 사용하여 독립적인 여러 개의 게임을 하나의 알고리즘을 통해 고정된 parameter로 학습하는 것이다. 입력은 high-dimensional하며, 게임의 종류는 다양하다. 좋은 해결책은 learning algorithm을 통해 학습하는 것이고, tuning하여 특정 domain에 대해 끼워 맞추는 것은 feasible하다.
Network Architecture는 3개의 convolution layer와 fully connected된 hidden layer를 지니는 CNN 구조이다. 또한 입력으로 마지막 4개의 frame을 사용하고 각 행동에 대한 action value를 output으로 보낸다. 각 게임에서 network는 200M frames에 대해 하나의 GPU로 학습되었으며, 약 1주일이 걸렸다.
[ Results on overoptimism ]

위의 그림은 6개의 Atari 게임에서 DQN의 overestimation에 대한 예제를 보여준다. DQN은 끊임없이, 때로는 과하게 current greedy policy에 대해 overoptimistic한데, 주황색 직선과 주황색의 학습곡선을 비교해보면 이를 확인할 수 있다. 이 그래프에서 y값은 best learned policy에 대한 actual discounted value이다. 그리고 각 value estimates는 $$\frac{1}{T}\sum_{t=1}^{T=125000}argmaxQ(S_t, a;\theta)$$ 로 계산한다.
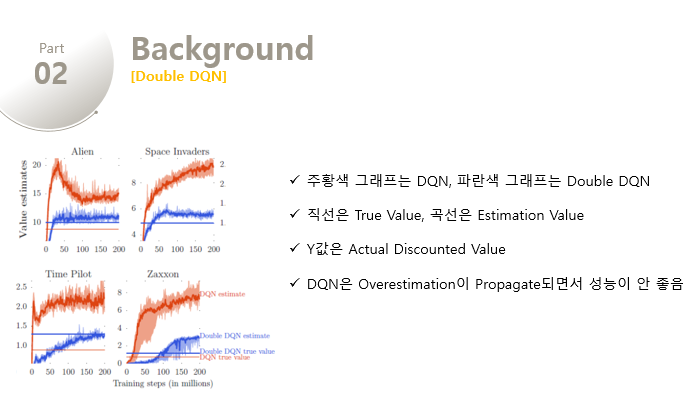

만약 overestimation이 없었다면, DQN의 Estimate는 직선에 근접하게 일치했을 것이다. 하지만 DQN의 학습곡선은 true value보다 계속해서 높게 위치함을 확인할 수 있다. 반면에 파란색의 Double DQN의 학습곡선은 Double DQN의 True Value직선에 더욱 근접함을 알 수 있다. 또한 파란색의 Double DQN의 직선은 주황색의 DNQ 직선보다 높은데, 이것은 Double DQN이 더욱 정확한 value estimate를 한다는 것 뿐만 아니라 더 좋은 policy를 제공함을 의미한다.
중간의 두 게임에서는 Overestimation이 더욱 심하게 발생함을 알 수 있는데, DQN은 상당히 불안정한 모습을 보인다. 해당 그래프의 y값은 log-scale의 value를 보여준다. 중간의 그래프에서 DQN의 value estimates가 증가함에 따라(Overestimation이 시작되면서) 아래의 그래프의 score가 하락함을 확인할 수 있다. 이를 통해 Overestimation이 resulting policy에 안좋은 영향을 미침을 알 수 있다. 해당 그래프가 instable한 것은 off-policy로 function approximation하는 학습 방법때문이라고 착각할 수 있다. 하지만 우리는 Double DQN에서 학습이 더욱 안정적임을 확인할 수 있고, 문제의 원인은 DQN의 Overestimation임을 확인할 수 있다. 또한 위의 그림의 게임을 포함한 모든 49개의 테스트 게임에서 overestimation이 확인되었다.
[ Quality of the learned policies ]
Overoptimism이 항상 learned policy의 quality에 악영향을 미치는 것은 아니다. 예를 들어, Pong 게임에서는 약간의 overestimation이 있었음에도 불구하고 최적의 behavior를 달성할 수 있었다. 그럼에도 불구하고 Overestimation을 줄이는 것은 안정적인 학습을 할 수 있게 도와주며 위의 그림들에서 이를 확인할 수 있다. 이제 우리는 Double DQN이 policy quality의 관점에서 얼마나 도움이 되는지 평가할 수 있다.
각각의 evalution epsiode는 different starting point를 제공하기 위해, 30번 까지는 환경에 영향을 주지 않는 sepcial no-option action을 실행함으로써 시작된다. 몇몇 exploration은 추가적인 randomization을 제공하기도 한다. Double DQN에서는 DQN과 같은 hyper-parameter를 사용하였고, overestimation을 줄이는데만 초점을 두었다. 학습된 policy들은 $\epsilon=0.0.5$ 를 지니는 greedy policy와 함께 5분(18000 frames)동안 평가된다. 점수들은 100개의 에피소드들에 대해 평균을 구한 값이다. Double DQN과 DQN의 차이는 target뿐이다. 이러한 evaluation 방식은 사용된 hyper-parameter가 Double DQN이 아닌 DQN에 맞춰지있기 때문에 적합하지 않을 수 있다.
점수를 nomalize하기 위해 아래와 같이 계산하였다. $score_{normalized} = \frac{score_{agent} - score_{random}}{score_{human} - score_{random}}$

위의 표는 Double DQN이 DQN을 능가했음을 보여준다.

[ Robustness to Human starts ]
이전의 evaluation에 대한 하나의 우려사항은 starting point가 하나인 determistic game에서는 학습자가 generalize할 필요성을 느끼지 않고, sequences of actions를 암기하도록 학습할 수 있다는 것이다. 이런 상황에서 결과는 성공적일 수 있지만, solution이 robust하지 않을 수 있다. 다양한 starting point에서 학습함으로써, 발견한 학습법이 잘 일반화되었는지 테스트할 수 있고, 학습된 policy에 대해 어려운 testbed를 제공할 수 있다.
우리는 human expert trajectory로부터 각 게임에 대해 100개의 starting point를 얻었다. 우리는 이 starting point로부터 evaluation episode를 실행하였고, 108000 프레임까지 eumlator를 실행하였다. 각각의 Agent는 starting point 이후에 누적된 reward만으로 평가되었다.
Evaluation을 위해 tuning한 version의 Double DQN을 포함하였다. 기존의 파라미터는 DQN에 맞춰주어져 있었기때문에, 때때로 tuning하는 것이 적합하기도 하다. tuning한 version의 Double DQN에서2개의 Network가 switch할때 마다 Q-learning으로 rever하기 때문에 overestimation을 줄이기 위해 우리는 2개의 복사된 network사이의 frame수를 증가시켰다. 또한 학습중에는 $\epsilon$ 을 0.1에서 0.01로 줄였고, evaluation에서는 해당 값을 0.001까지 줄였다. 최종적으로 tuned version은 0.001이라는 하나의 shared bias를 갖게 되었다. 그리고 이러한 변화는 performance를 높이고, 더 좋은 결과를 보여주었다.
그리고 Table2를 통해 Double DQN이 더욱 generalize하게 학습되었을 알 수 있다.
5. Discussion
이 논문은 5개의 contribution을 한다.
-
Q-learning이 왜 large-scale problem에서 overoptimistic될 수 있는지를 보여준다.
-
Atari game에서 value estimation을 분석함으로써, overestimation은 common하며 꽤나 심각함을 보여준다.
-
Double Q-learning은 이러한 overoptimism을 줄이기 위해 사용될 수 있으며, stable하고 reliable한 학습을 할 수 있다.
-
추가적인 network나 parameter 없이 기존의 architecture와 DQN의 네트워크를 사용하는 Double DQN을 보여준다.
-
Double DQN은 더 좋은 policy를 찾고, 2600개의 게임이 있는 atari에서 state-of-art한 결과를 얻을 수 있다.
논문의 전체 PPT를 받기 원하시면 첨부파일을 참고해주세요!
참고 자료
- https://ishuca.tistory.com/396
- https://jsideas.net/drlnd_issues_in_using_function_approximation
- https://steemit.com/deep-learning/@backhoing/deep-reinforcement-learning-with-dobule-q-learning
- https://ishuca.tistory.com/396
- https://parkgeonyeong.github.io/Double-DQN%EC%9D%98-%EC%9D%B4%EB%A1%A0%EC%A0%81-%EC%9B%90%EB%A6%AC/
'인공지능' 카테고리의 다른 글
| [논문번역] Playing Atari with Deep Reinforcement Learning 논문 설명/요약 (2) | 2020.02.10 |
|---|---|
| E-Greedy Algorithm(입실론 그리디 알고리즘)이란? (4) | 2020.02.10 |
| 마르코프 의사결정 모델(MDP)이란? (0) | 2020.02.09 |
| Experience Replay Memory란? (0) | 2020.02.09 |
| Stochastic Gradient Descent(SGD)란? (0) | 2020.02.09 |


